こんにちは、 @kz_morita です。

情報検索のシステムについて勉強中で，以下のような記事をこれまでにまとめました．

• 情報検索の概要について
• 情報検索と転置インデックスについて
• 検索システムと辞書・用語

今回はワイルドカードのクエリについてまとめます．

ワイルドカードクエリとは

ワイルドカードクエリとは，以下のようなクエリのことを指します．

pro*ing

このようなクエリに対して，programming や，processing などといったワードで検索したような文書を返すことを目的にしたものです．

このような検索を実現するための手法について見ていきます．

辞書とデータ構造

その前に，検索システムにおける語彙とそれを扱うデータ構造についてまとめます．

検索システムでは，検索されたワードに対して一定の正規化などを行った後にそのワードを辞書から見つけ出す必要があります．辞書から見つければその後は，ポスティングリストを参照し文書IDを得るといった流れになります．

辞書から見つけるのには，通常の全探索だと語彙数を N としたときに O(N) の計算量となります． 効率よく探すために以下のようなデータ構造が用いられます．

• ハッシュ
• 探索木

ハッシュ

ハッシュは，用語を特定のハッシュ関数でハッシュ化して格納するもので，計算量は (ハッシュ計算する時間を除いて) O(1) になり高速です．

ただし，デメリットもあります．

まず，ハッシュの衝突です．ハッシュの計算結果は十分大きい数の数値のため通常は衝突を気にするケースはあまりありませんが，Web 検索システムなど扱う語彙の数が膨大なシステムnの場合は，本当に衝突を気にする必要がないかどうかをよく検討する必要がありそうです．

２つめに，似ている語彙を探すことが困難なことがあります．語彙がすこしでも違えば，まったく別のハッシュ値になることも普通にありえるので柔軟的に扱うのは難しいです．

探索木

探索木は，データを木構造で扱うことで O(logN) の計算量で探索できるようにしたものです．

以下のようなものが代表的です．

• 二分木 (binary-tree)
• B 木 (B-tree)

詳細はここでは扱いませんが，検索システムでは，B-tree が用いられることが多いそうです．

B-tree については，下記のサイトなどがわかりやすかったです．

ワイルドカードクエリの実現方法

後方一致

まずは，以下のような後方一致のワイルドカードクエリについて考えます．

prog*

後方一致のクエリに関しては，以下の図のように 探索木を辿っていって prog までたどれたらその子供の木でアクセスできる用語すべてのリストが用語リストになります．

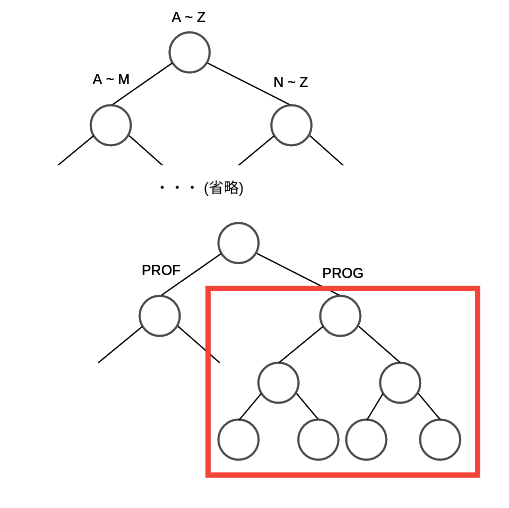
この用語のリストの論理積のクエリととらえて，あとは転置インデックスから文書IDを取得すれば prog* の検索を実現できます．

前方一致

たとえば，以下のようなクエリを考えます．

*ing

これは，用語を逆順に格納した，リバース B-tree を考えれば実現することが出来ます．

予め語彙を逆順にしたものをTreeに保持しておいて gni* というクエリで探すという形です．

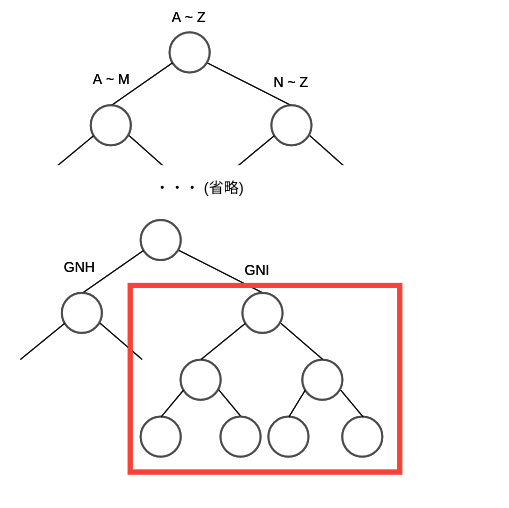
こうすることで，後方一致と同じように検索が可能です．

間にワイルドカードが挟まった形

以下のようなクエリの場合です．

prog*ing

この場合は，クエリを prog* と *ing と分けて考え，それぞれ後方一致と前方一致で用語リストを得たあとに，それぞれのリストの論理積をとることで実現できます．

順序入れ替え用語語彙

上記では，前方一致と後方一致で考えましたが，順序入れ替え用語語彙 を用いる方法では，用語を回転したものを拡張して順序入れ替え用語語彙の集合として保持することで実現します．

具体的に，computer という文字列で考えると以下のようになります．

• 末尾に終端文字をつける

computer => computer$

• 回転させる

computer$
omputer$c
mputer$co
puter$com
uter$comp
ter$compu
er$comput
r$compute
$computer

• 回転させた各ワードから元の computer への参照を保持する

それでは実際の動きを c*r というクエリで，car と computer が見つかるまでの例を用いて説明します．

• 検索クエリをワイルドカードが後ろに来るように回転させる

c*r => r$c*

• あらかじめ回転させておいた順序入れ替え用語語彙 の集合から探す

computer$
omputer$c
mputer$co
puter$com
uter$comp
ter$compu
er$comput
r$compute <-- r$c* に hit!
$computer

car$
ar$c
r$ca <-- r$c* に hit!
$car

上記のような手順で，c*r というクエリで, car や computer を見つけることが出来ます．

k グラムインデックス

上記の順序入れ替え用語語彙では，シンプルにワイルドカードを見つけることができるのですが，順序入れ替え用語語彙の集合がかなり大きなサイズになります．

そこで，単語を kグラムに分割してワイルドカード検索を実現する方法があります．

k グラムとは k 個の文字の並びのことで，たとえば computer という単語の 3グラムは以下のようになります．

com
omp
mpu
put
ute
ter

単語の最初と最後を識別できるように，拡張すると以下のようになります．

$co
com
omp
mpu
put
ute
ter
er$

k グラムで検索を実現するために，kグラムインデックスを予め構築します． これは，k グラムから，用語リストを参照できるようにしたインデックスになります．具体的には以下のような感じです．

mpu => computer, impulse, tempura ...

これらを用いて，com* というワイルドカードクエリで検索する流れを説明します．3 グラムの例で説明します．

手順としては以下のような感じです．

• ワイルドカードクエリを，3グラムに分割する
• 3グラムのクエリを，kグラムインデックスを用いて用語リストを得る
• ポストフィルタリング
• 転置インデックスで文書 ID を得る

ワイルドカードクエリを，3グラムに分割する

com* というクエリを以下のように分割します．

• $co
• com

3グラムのクエリを，kグラムインデックスを用いて用語リストを得る

k グラムインデックスを用いて，$co AND com という条件で，用語リストを得ます．

以下のような用語リストが得られたとします．

• computer
• compress
• concomitance

ポストフィルタリング

kグラムインデックスから用語を得ましたが，concomitance という単語は，com* というクエリには，マッチしていないのにもかかわらず検索に引っかかってしまっています．

そのため，このポストフィルタリングの手順では，得られた用語リストを更に，元のクエリである com* で grep し，フィルタリングします．

• o: computer
• o: compress
• x: concomitance

転置インデックスで文書 ID を得る

ポストフィルタリングのステップで，computer , compress という用語が得られたので，computer, compress という用語で転置インデックスから，文書IDを取得し，それぞれの文書 ID 集合の論理積をとれば結果を得ることが出来ます．

まとめ

今回は，ワイルドカードクエリの仕組みについて簡単にまとめました．ワイルドカード検索の手法をいくつかまとめましたが，かなりコストのかかる処理になってしまうのは間違いないため，そもそも対象とする検索システムに導入するかどうかという点も検討する必要がありそうです．

ただ，このようにワイルドカード検索を実装するために，いくつかのデータ構造を検討し処理を効率化するプロセス自体はとても工夫がなされていて参考になるし，とてもおもしろいものだと思います．

参考

• 情報検索の基礎