blog.foresta.me

Elixirで線形回帰してみた

2017年12月2日 engineering

この記事はElixir Advent Calendar 2017の17日目の記事です。

最近始めたElixirで何かOutputしたいということで線形回帰のアルゴリズムを実装してみました。

リポジトリはこちら https://github.com/foresta/mlex.git

Elixirでも機械学習できないこともない（かもしれない）ことを書いていこうかなと思います。

背景

最近の私の興味があるものとしてEilxirと機械学習があります。

Elixirはサンプルアプリや簡単なツールを制作した程度、機械学習はcourseraのコースを一通りやり本を数冊読んだ程度です。

今回はその両方の学習と、どうせ機会学習アルゴリズム実装するなら書きごごちの良いElixirで書いてみたいと思い実装してみました。

線形回帰とは

データを元に線形モデルを作成しその線形モデルを用いて未知のデータを予測するものです。

図1はデータの次元が2次元の場合の線形回帰の概念を示し、×印が与えられたデータ、直線が学習した結果の線形モデルを表しています。

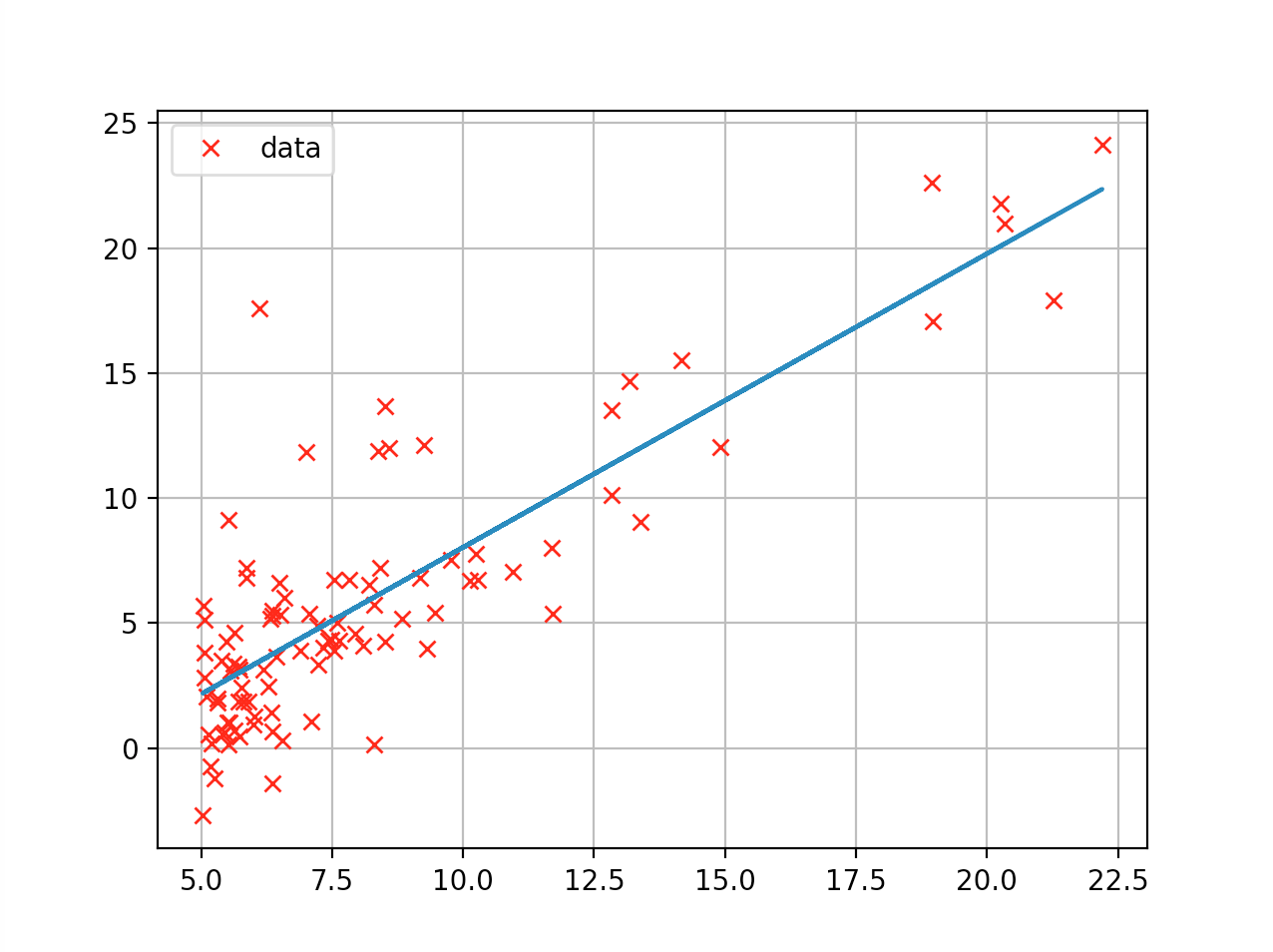
図1 線形回帰のサンプルグラフ

詳しくはこちらのサイトを参照してください。

学習データ

今回学習には以下のデータセットを使用しました。

linnerud_physiological.csvには体重・ウエスト・心拍数等の身体的特徴データが、 linnerud_exercise.csvには懸垂・腹筋・跳躍に関するデータがあります。

今回は身体的特徴と、懸垂のデータで線形回帰をしてみます。

実装

使用したライブラリは以下のような感じです。

defp deps do
  [
    {:matrix, "~> 0.3.0"},
    {:csv, "~> 2.0.0"},
    {:explotter, git: "https://github.com/foresta/explotter.git"}
  ]
end

ソースコードは以下のような感じです。

mlex/apps/sample/lib/linnerud.ex

def run do
  # 1. load dataset
  features = load_linnerud_feature_dataset()
  targets = load_linnerud_target_dataset()

  # 2. setup featuresex
  pulses = features[:pulse]
  waists = features[:waist]
  weights = features[:weight]
  number_of_data = length pulses
  bias = for _times <- 1..number_of_data, do: 1.0

  x = [bias, weights, waists, pulses]
  x = Matrix.transpose(x)

  # 3. setup targets
  y = [ targets[:chins] ]
  y = Matrix.transpose(y)

  # 4. setup gradientDescent params 
  alpha = 0.00003
  iterations = 10000
  theta = [[0], [0], [0], [0]]

  # 5. train
  theta = LenearRegression.gradientDescent(x, y, theta, alpha, iterations)
  # test
  x_test = [[1],[191],[36],[50]]
  y_test = [[5]]

  # 6. predict
  predicted_chins = LenearRegression.predict(Matrix.transpose(x_test), theta)

  # conpute cost
  error = LenearRegression.computeCost(x_test, y_test, theta)

  IO.puts "===== test data ====="
  IO.puts "x: "
  IO.inspect x_test
  IO.puts "y: "
  IO.inspect y_test
  IO.inspect predicted_chins
  IO.inspect error
end

実際の学習処理はlinner_regression.exにあってそれぞれ以下の数式を実装しています。

predict/2

線形モデルを表す関数。 https://github.com/foresta/mlex/blob/master/apps/lenear_regression/lib/lenear_regression.ex#L6

$$ h_{\theta}(x) = \theta_{0}x_{0} + \theta_{1}x_{1} + \cdots + \theta_{n}x_{n} = \theta^{T}x $$

computeCost/3

実際の仮説関数の結果と、実際のデータとの間の誤差を表す関数。 https://github.com/foresta/mlex/blob/master/apps/lenear_regression/lib/lenear_regression.ex#L10

$$ J(\theta) = \frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)})^{2} $$

gradientDescent/5

https://github.com/foresta/mlex/blob/master/apps/lenear_regression/lib/lenear_regression.ex#L23

最急降下法を用いてパラメータθを学習する関数。

Repeat { $$ \theta = \theta - \alpha \frac{1}{m} \sum_{i=1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)})x^{(i)} $$ }

結果

実行すると以下のようになります。

mlex > iex -S mix
Erlang/OTP 20 [erts-9.1.2] [source] [64-bit] [smp:8:8] [ds:8:8:10] [async-threads:10] [hipe] [kernel-poll:false] [dtrace]

==> sample
Compiling 1 file (.ex)
Interactive Elixir (1.5.2) - press Ctrl+C to exit (type h() ENTER for help)
iex(1)> Linnerud.run
====== test data =====
x:
[[1, 191, 36, 50]]
y:
[[5]]
===== pridiction =====
[[7.768239007142219]]
error:
3.8315736003318683
3.8315736003318683
iex(2)>

結果より正解が5のテストデータに対して、約7.77と予測しています。 一応学習できているっぽいです。 が、データ量が少なく、十分な訓練/テストデータが用意できていないためこれが良い精度なのか悪い精度なのか判別は難しいと考えます。

パッと思いつくだけでも、以下の改良点が考えられます。

  • データ量が増やす
  • データセットのスケーリングをする
  • 正則化する

参考

まとめ

まず、ElixirのAdventCalendarなのに機械学習の話題がメインばかりになってしまった気がして反省してます。

Elixirふわりとしか触っていなかったのですが、アルゴリズムの実装は割とサクサクでき非常に触りごごちの良い言語だなぁと改めて実感しました。

Elixirは書いてて楽しいので、他のアルゴリズムやアプリケーションなどもっと 書いていきたいと思いました。

  • Elixirで線形回帰のアルゴリズムを書いてみた
  • ロジックはかけることはかける(行列の扱いがやや大変)
  • 大量のデータセットでも実用的なパフォーマンスがでるかは要検証
  • Elixir楽しい(重要)
この記事をシェア

関連記事