こんにちは、kz_moritaです。
最近競技プログラミングを再度やり始めて悪戦苦闘しています。
本記事では、ナップサック問題を実際に解いてみます。
ナップサック問題とは?
今回の対象となるナップサック問題ですが、Wikipediaにはこう書かれています。
ナップサック問題(ナップサックもんだい、Knapsack problem)は、計算複雑性理論における計算の難しさの議論の対象となる問題の一つで、「容量 C のナップサックが一つと、n 種類の品物(各々、価値 pi, 容積 ci)が与えられたとき、ナップサックの容量 C を超えない範囲でいくつかの品物をナップサックに詰め、ナップサックに入れた品物の価値の和を最大化するにはどの品物を選べばよいか」という整数計画問題である。
要するに、特定の容量が決まっているナップサックにお宝を目一杯詰めたい時に、お宝の価値が最大になる組み合わせを求めるっていう問題ですね。
出来るだけ価値が高いお宝を詰めたいけども、あまり容量の大きな物を入れると数が入らなくなってしまうというトレードオフをうまいこと求めようというものです。
普通に解いてみる
それでは、まずは普通に解いてみます。
前提条件
今回の例として以下のような条件で考えてみます。
- ナップサックの容量
- 10
- アイテム
- 5種類
| 重さ | 価値 | |
|---|---|---|
| Item1 | 3 | 2 |
| Item2 | 4 | 3 |
| Item3 | 1 | 2 |
| Item4 | 2 | 3 |
| Item5 | 3 | 6 |
考え方
ナップサック問題を解くにあたり、以下のような木構造を考えます。

Itemをナップサックに入れるか入れないか、という分岐を木構造で表現してみます。
すると、各ノードで価値と重さそれぞれの合計を計算することができます。
価値と重さを計算した結果を以下に載せます。
(weight, value) という記述形式て各ノードの計算された数を表しています。
例えば、初期状態が (0, 0) で Item1 をナップサックに入れると、 (3,2) になり、さらに Item2 をナップサックに入れると (7,5) になるといった様子をみることができます。
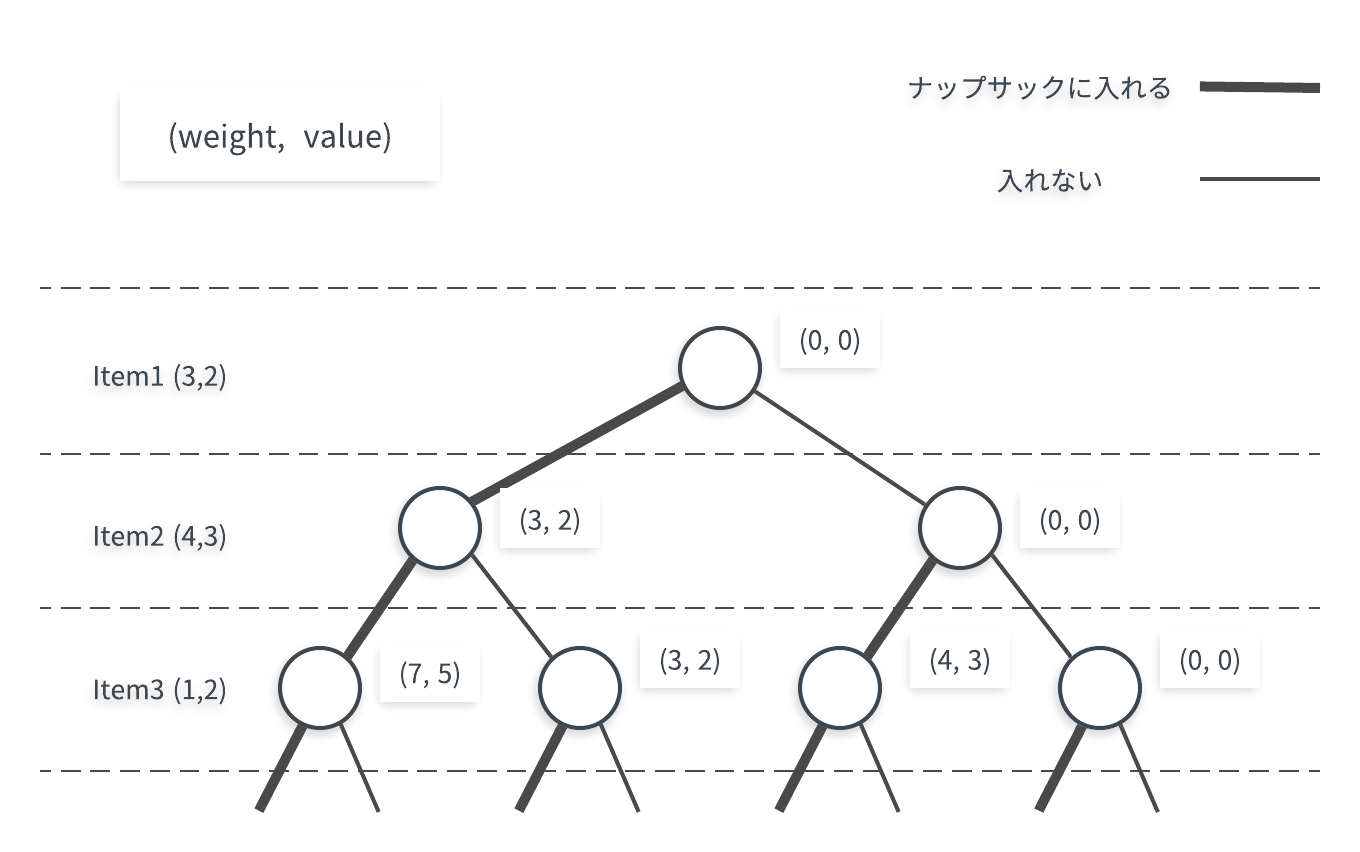
上記の図からナップサック問題を解くには、 weightがナップサックの容量を超えない 範囲で、 valueが最大になる ようなノードを探索すれば良いことになります。
実装
それでは、まず全探索するプログラムを書いてみます。
言語は c++14 を用います。
深さ優先探索で実装してみました。
#include <iostream>
#include <vector>
#include <numeric>
using namespace std;
struct Item {
int weight { 0 };
int value { 0 };
};
vector<Item> items {
{ 3, 2 },
{ 4, 3 },
{ 1, 2 },
{ 2, 3 },
{ 3, 6 }
};
int totalValue = 0;
int capacity = 10;
void knapsack(int value, int weight, int index) {
// Check capacity
if (weight > capacity) return;
// Update totalValue
totalValue = max({ totalValue, value });
// Check item size
if (items.size() <= index) return;
Item item { items[index] };
// Put in a bag
knapsack(value + item.value, weight + item.weight, index+1);
// Don't put in a bag
knapsack(value, weight, index+1);
}
int main() {
knapsack(0,0,0);
cout << totalValue << endl;
return 0;
}
上記コードでは、深さ優先探索で各ノードを探索していってます。 探索の終了条件は以下の通りです。
- 合計の重さがナップサックの容量を超えること
- 木の深さのチェック (アイテムの数を超えないように)
実行すると結果は 14 となり、 (weight, value) = (4, 3), (1, 2), (2, 3), (3, 6) を選択した時の、重さ10, 価値14が最大であることがわかります。
課題感
今回は、ナップサック問題を再帰で実装しましたが、この方法だと辺の数だけ再帰関数を呼ぶ必要があるため計算量が多くなってしまいsます。 次回にメモ化再帰という方法を使って同じ問題を解いてみます。
まとめ
今回は愚直に実際にナップサック問題を解いてみました。 次回をこの計算量を削減する方法を説明していこうと思います。