データの集合を見るときにどの様な傾向があるのか、またデータ集合同士を比較などしたいときに、用いられるのが代表値です。 (統計量とも呼ばれます)

具体的にいうと、データセットAとデータセットBどちらが大きいか？という問いに対して、「平均」という代表値を用いA,Bの平均を比較することによって答えることができます。

データには量的データと質的データがある (記述統計学とデータについて参照) ので、それぞれで主な代表値をまとめます。

データの準備

Irisのデータを使用しながら、各代表値を見ていくので準備をします。
今回は sepal length (cm) のみを使用することにします。

import pandas as pd
from sklearn import datasets

iris = datasets.load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
sepal_lengths = pd.Series(df['sepal length (cm)'])

代表値 ~量的データ~

算術平均 (mean)

いわゆる一般的な平均。

$$ 算術平均 = \frac{全データの総和}{データ数}
$$ $$ \overline{x} = \frac{\sum^{n}_{i=1}x_{i}}{n} $$

python実装

sepal_lengths.mean()
# => 5.843333333333334

トリム平均 (trimmed_mean)

外れ値の影響を受けないようにするために、異常値を取り除いた平均です。
もっとも小さい値からp個, もっとも大きい値からp個取り除いたデータ集合をxを整列したものを
$x_{(i)}: x_{(1)}, x_{(2)}, x_{(3)}, …, x_{(n)}$
で表すと

$$ トリム平均 = \frac{取り除いた後のデータの総和}{取り除いた後のデータ数} $$ $$ \overline{x} = \frac{\sum^{n-p}_{i=p+1}x_{(i)}}{n-2p} $$

python実装

new_sepal_lengths = sepal_lengths

# 外れ値を追加して見る
new_sepal_lengths[150] = 100000

# 平均を計算
new_sepal_lengths.mean()
# => 668.0562913907285
# 外れ値に平均が引っ張られている

from scipy import stats

# 上下１０％をトリムして平均を計算
stats.trim_mean(new_sepal_lengths, 0.1)
# => 5.822314049586778

加重平均 (weighted mean)

重みのデータ$w_{i}$を用いて

$$ 加重平均 = \frac{データ×重みの総和}{重みの総和} $$

$$ \overline{x_{w}} = \frac{\sum^{n}_{i=1}w_{i}x_{i}}{\sum^{n}_{i=1}w_{i}} $$

python実装

import numpy as np

iris = datasets.load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
sepal_lengths = pd.Series(df['sepal length (cm)'])

# 重み配列
w = np.random.rand(sepal_lengths.count())

# 加重平均を計算
np.average(sepal_lengths, weights=w)
# => 5.875578300988546

幾何平均 (geometric mean)

$$ 幾何平均 = \frac{データ×重みの総和}{重みの総和} $$

$$ m_g = \sqrt[n]{\prod_{i=1}^{n}x_i} $$

python実装

from scipy import stats

stats.gmean(sepal_lengths)
# => 5.785720390427728

調和平均 (harmonic mean)

調和平均H

$$ \frac{1}{H} = \frac{1}{n}(\frac{1}{x_1} + \frac{1}{x_2} + \frac{1}{x_3} + \cdots + \frac{1}{x_n}) $$ $$ H = \frac{n}{\frac{1}{x_1} + \frac{1}{x_2} + \frac{1}{x_3} + \cdots + \frac{1}{x_n}} $$ $$ H = \frac{n}{\sum_{i=1}^{n}\frac{1}{x_i}} $$

python実装

from scipy import stats

stats.hmean(sepal_lengths)
# => 5.728905057850834

平均絶対偏差 (mean absolute deviation)

平均値からの偏差(各データの差分)の平均。

$$ 平均絶対偏差 = \frac{\sum^{n}_{i=1}|x_{i}-\overline{x}|}{n} $$

python実装

sepal_lengths.mad()
# => 0.6875555555555557

分散 (variance)

平均からの偏差の二乗和でデータの総数で割ったもの。

$$ 分散 = s^2 = \frac{\sum^{n}_{i=1}(x_i-\overline{x})^2}{n} $$

python実装

np.var(sepal_lengths)
# => 0.6811222222222223

標準偏差 (standard deviation)

標準偏差: 分散の平方根

$$ 標準偏差 = s = \sqrt{分散} $$

np.std(sepal_lengths)
# => 0.8253012917851409

代表値 ~質的データ~

中央値 (median)

中央値は上下に全データの半分ずつデータが存在するような値です。
カテゴリデータには使えません。

python実装

sepal_lentghs.median()
# => 5.8

最頻値 (mode)

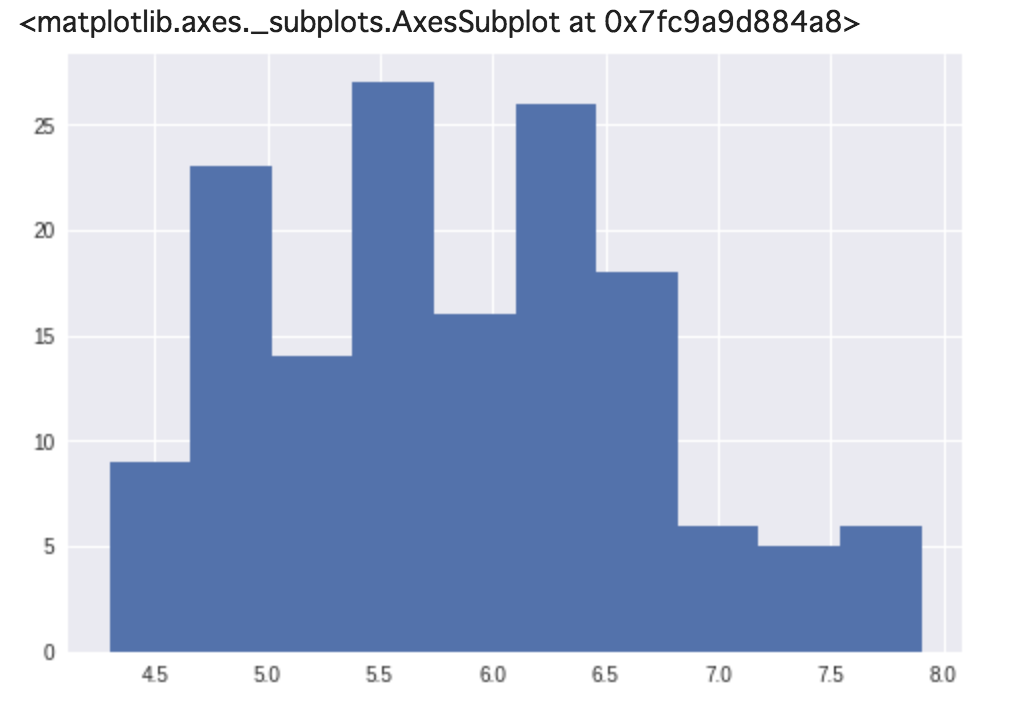
最頻値は度数分布表やヒストグラムの一番度数が大きい (もっとも頻繁に現れる) データの値です。

以下のヒストグラムの左から４番目の値、つまり (5.38, 5.74] が最頻値となります。

python実装

# 10区間にビニング
binned_sepal_lengths = pd.cut(sepal_lengths, 10)

print(binned_sepal_lengths.value_counts().sort_index())
# =>
# (4.296, 4.66]     9
# (4.66, 5.02]     23
# (5.02, 5.38]     14
# (5.38, 5.74]     27
# (5.74, 6.1]      22
# (6.1, 6.46]      20
# (6.46, 6.82]     18
# (6.82, 7.18]      6
# (7.18, 7.54]      5
# (7.54, 7.9]       6

print(binned_sepal_lengths.mode())
# => 0    (5.38, 5.74]

その他

中央値絶対偏差

(MAD: Median Absolute Deviation fomr in the median)
中央値は平均とは違い、異常値に影響されにくい性質 (=ロバスト性) がある。

m = 全データの中央値として $$ MAD = 中央値(|x_1-m|,|x_2-m|,…,|x_n-m|) $$

python実装

# 平均絶対偏差
print(sepal_lengths.mad())
# =>0.6875555555555557

# 外れ値を追加して見る
sepal_lengths[150] = 100000

# 再び平均絶対偏差
print(sepal_lengths.mad())
# => 8137.409105840147

# 中央値絶対偏差
np.median(abs(sepal_lengths - np.median(sepal_lengths, axis=0)), axis=0)
# => 0.7000000000000002

まとめ

• 代表値はデータを表す値
• データの性質や用途によってどの代表値を用いるかを考える必要がある
• numpy, scipyなどのエコシステムなどに標準搭載されていて最高