相関係数について
相関係数は二つの変量どうしの関係性について知りたい時に用いられる統計量です。
相関係数には、正の相関関係と負の相関関係があります。 片方の変量が増えた時に、もう片方の変量も比例して増えていく時には正の相関関係があり、一方が増えるともう一方が減る傾向があるときは負の相関関係があると言えます。
例えば、身体データの身長と体重という二つの変量の相関は 一般的に身長が大きい人の方が体重が重くなりやすいだろうと考えられ、その場合には身長と体重には正の相関関係があるといえます。
相関係数はこの相関関係の度合いを表す変量となっています。
相関係数の式は以下のようになっています。
$$ 相関係数 r = \frac{\sum^{n}_{i=1}(x_i - \overline{x})(y_i - \overline{y}) }{\sqrt{\sum^{n}_{i=1}(x_i - \overline{x})^2} \sqrt{\sum^{n}_{i=1}(y_i - \overline{y})^2}} $$
この相関係数 r は $-1 \le r \le 1$ となっており、1に近いほど正に強い相関関係があり、-1に近いほど負に強い相関関係があります。
Pythonでの実装
それでは実際にPythonでデータの相関について見ていきます。
データはIrisのデータを使用します。 環境は今回も、Google Colabratoryを使用しています。
まずはデータの準備から。
import pandas as pd
from sklearn import datasets
iris = datasets.load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
相関を計算するには以下のようにします。
df.corr()
すると以下の様に表示されるかと思います。
| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | |
|---|---|---|---|---|
| sepal length (cm) | 1.000000 | -0.109369 | 0.871754 | 0.817954 |
| sepal width (cm) | -0.109369 | 1.000000 | -0.420516 | -0.356544 |
| petal length (cm) | 0.871754 | -0.420516 | 1.000000 | 0.962757 |
| petal width (cm) | 0.817954 | -0.356544 | 0.962757 | 1.000000 |
散布図をプロットしてみます。
import matplotlib.pyplot as plt
plt.scatter(df['sepal length (cm)'], df['sepal width (cm)'])
plt.show()
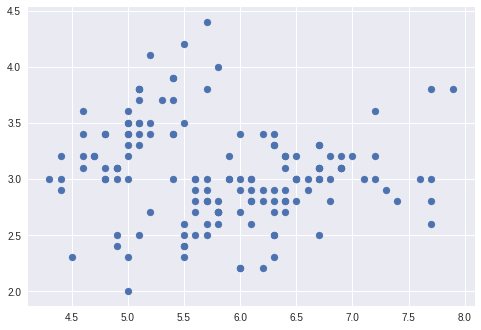
一つ一つ散布図を見るのではなく、散布図行列を出してくれるメソッドもあるのでそっちも使って見ます。
from pandas.tools.plotting import scatter_matrix
import matplotlib.pyplot as plt
scatter_matrix(df, diagonal='hist', grid=True)
plt.show()
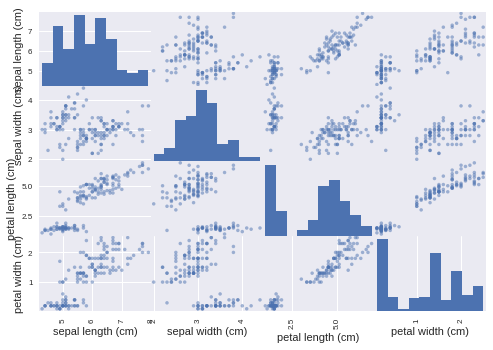
相関をヒートマップで表して見ます。
import pandas as pd
import seaborn as sns
# ヒートマップで表示
sns.heatmap(df.corr(), square=True, vmax=1, vmin=-1, center=0)
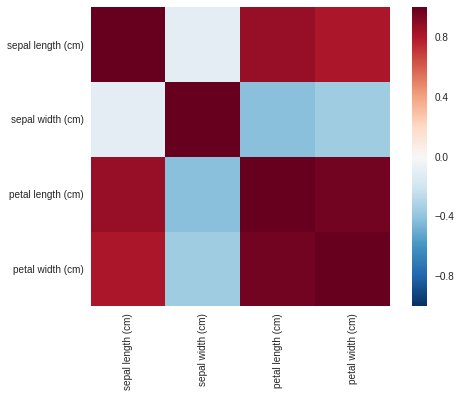
まとめ
- 二つの変量の関係性をみるのに相関が便利
- Pythonのエコシステムには色々な便利な関数が用意されている
- データの性質を見るために相関などをみることが重要