こんにちは、 @kz_morita です。

今回は，検索エンジンなどの，クエリと文書のマッチ度に使われる BM25 の式を読み解いていきます．

BM25 とは

BM25 は，検索システムにおいて，クエリが文書とどれだけマッチしているかについてを計算するための手法になります．

式で表すと以下になります．

$$ score(D, Q) = \sum^{n}_{i=1} IDF (q_i) \cdot \frac{f(q_i, D) \cdot (k_1 + 1)} {f(q_i, D) + k_1 \cdot (1 - b + b \cdot \frac{|D|}{avgdl})} $$

これらの式の意味を一つずつ見ていきます．

各種変数の意味

上記の式の score 関数に登場する各種変数について見ていきます．

D

検索対象の特定の文書の文字列集合

|D|

検索対象の特定の文書の文字列集合の大きさ (どれくらいの単語量 ≒ 文書量) なのか

avgdl

全文書の文字列集合の大きさの平均

Q

検索クエリの文字列集合

q

検索クエリの１つの単語

IDF関数

Inverse Document Frequency の略．いろんな文書に登場する一般的な単語だと値が小さく，レアな単語だと値が大きい

f 関数

検索クエリの単語が対象の文書の中でどのくらい現れるかの指標．tf (Term Frequency) であったり，純粋な数のカウントだったりする．tf の場合は，以下のような式になる

$$ tf = \frac{ある単語の出現回数}{全単語の合計数} $$

$k1$ と $b$ に関してはこの式の挙動を制御するためのパラメータになります．式を深堀しながらこれらのパラメータの役割も見ていきます．

式の理解

上記の式を大まかにみると以下のような構成になっていると思います．

$$ score(D, Q) = \sum_{i=1}^n IDF(q_i)\cdot A $$

$$ A = \frac{f(q_i, D) \cdot (k_1 + 1)} {f(q_i, D) + k_1 \cdot (1 - b + b \cdot \frac{|D|}{avgdl})} $$

A の式の中が難解そうなので，一旦大枠を考えると，score 関数は，検索クエリの単語ごとに $IDF(q_i) \cdot A$ を計算し加算しています．

IDF 関数は，単語がレアなほど大きな数値になるような関数なので，検索クエリの単語ごとに A の結果に重みをつけています．

これは，どの文書でもでてくるような汎用的な単語より，めったに文書にでてこない珍しい単語で検索にマッチしたときのほうがそのスコアを大きくするということで，検索のロジックとして直感的に妥当そうです．

あとは，検索クエリの単語と文書とのマッチ度である A の中身を解読すれば式全体の意味がわかりそうです．

A の式を再掲すると

$$ A = \frac{f(q_i, D) \cdot (k_1 + 1)} {f(q_i, D) + k_1 \cdot (1 - b + b \cdot \frac{|D|}{avgdl})} $$

で f 関数は，単語の出現頻度で，k と b がパラメータでした． $\frac{|D|}{avgdl}$ の部分は，文書の単語数 を 全文書の平均単語数で割っているので，相対的に対象の文章が長いのか短いのかを見ている部分になります．この部分が 1 であれば，平均と同じ文書量であり，2 であれば，2倍の文書量，$\frac{1}{2}$であれば，半分の文書量ということになります．

ここで，仮に，文書量を平均値．つまり，$\frac{|D|}{avgdl} = 1$ と固定してみます．

そうすると，Aの式は

$$ A = \frac{f(q_i, D) \cdot (k_1 + 1)} {f(q_i, D) + k_1 \cdot (1 - b + b \cdot 1)} = \frac{f(q_i, D) \cdot (k_1 + 1)} {f(q_i, D) + k_1} $$

となります．

この式を fの値を変数として，$k =1$ をパラメータとしてプロットしてみると以下のようになります．

グラフから，f関数の値 が増えれば増えるほど score も増やすけど，多くても k + 1 (つまり2) に漸近する程度になるという式なことがわかります．

ためしに，k = 3 などとしてみると，f の数が増えると，4 に漸近するようなグラフになります．

つまり，k の値は，スコアの上限値を決めるパラメータ となります．k の値が大きれば大きいほど，出現頻度である f 関数によって大きな差が生まれます．

さて，残りよくわかってないのが $ (1 - b + b \cdot \frac{|D|}{avgdl})$ の部分になります．

先程は，$\frac{|D|}{avgdl} = 1$ としましたが，ここでは ここの値もパラメータとして式を見ていきます．

$\frac{|D|}{avgdl} = 0.5$ つまり，文書量が平均の半分のときは以下のようなグラフになります．

つぎに $\frac{|D|}{avgdl} = 2$ つまり，文書量が平均の2倍のときは以下のようなグラフになります．

つまり，文書量が多いほど f関数の値によるスコアの上昇率が，緩やかになっています．

これは，クエリにヒットした文書のうち，文書量が少ないのにもかかわらずヒットした文書のほうがマッチ度合いが高いという意味になっています．文書量が多ければ含まれる単語の種類も増え検索クエリには必然的にマッチしやすくなるので文書量が少ないのにヒットした文書のほうを重視するというのは直感的にも正しそうです．

最後に残ったパラメータの b ですが，これは先程の 文書量に応じたペナルティの度合いを調整するためのパラメータ になります．

以下は，$\frac{|D|}{avgdl} = 2$ で固定し b の値を，0.5, 1, 2, 3 と動かしたときのグラフになります．

• 0.5: 紫
• 1: 赤
• 2: 青
• 3: 緑

b の値が大きければ大きいほど，文書量によるペナルティを受けスコアが上がりづらくなっていることがわかります．

もとの式を再掲します．

$$ score(D, Q) = \sum^{n}_{i=1} IDF (q_i) \cdot \frac{f(q_i, D) \cdot (k_1 + 1)} {f(q_i, D) + k_1 \cdot (1 - b + b \cdot \frac{|D|}{avgdl})} $$

これまで見てきたことをまとめると以下のようになります．

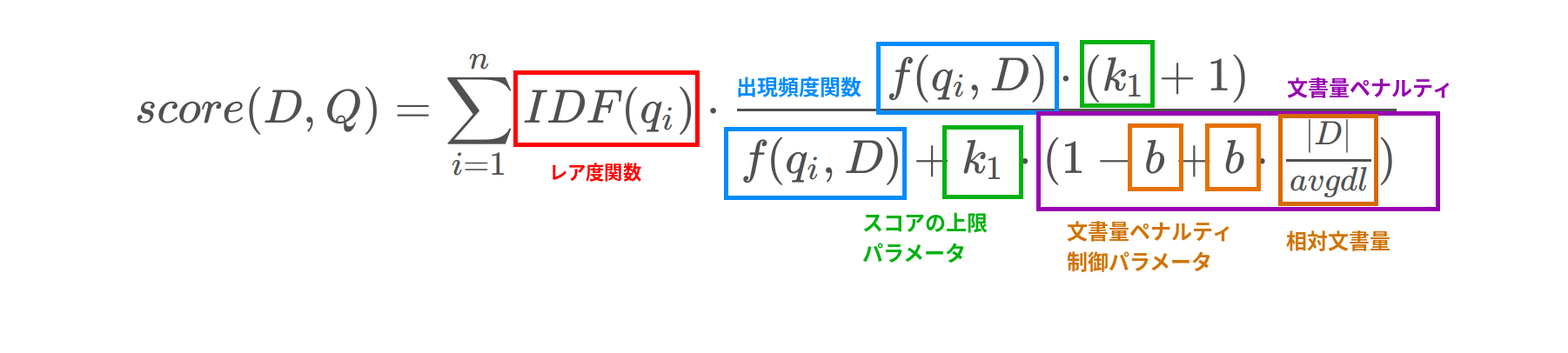
まとめ

今回は，BM25 の式について深堀りしました．一見複雑な式でしたが，ひとつずつ見ていくとパラメータによってうまく検索のマッチ度を考慮されていて，うまくできてるなぁと改めて思いました．

式から意図を読み解くと，どういう目的で使われるかしっかりわかるので数式を読み解くのはしっかり習慣にしていきたいと思います．