こんにちは、 @kz_morita です。
今回は、アルゴリズムの評価軸である計算量、そしてよく使われるオーダー記法についてまとめていきます。
アルゴリズムとは?
アルゴリズムというワードはよく聞くことが多いと思いますが、以下のように定義されていることが多いようです。
アルゴリズムとは、ある問題を解くのに
計算機などで機械的に解ける有限個の命令からなるプログラムであり、問題のいずれの入力に対しても、有限時間で正しい解を出して停止するものである
要は、問題を解くために、普通のプログラムのように任意の数の命令でかけて、無限ループしたり間違った答えを出さないものという感じの定義になります。
よく例に出されるのが、任意の要素を持つリストをソートするといったアルゴリズムがあると思います。
上記の定義に照らし合わせると、どんなリストを与えられても、有限個の命令で、(理論上) 有限時間で期待したソート順を返すのが、ソーティングアルゴリズムということが言えそうです。
以下のようなソーティングアルゴリズムを一度は聞いたことがあるのではないでしょうか?
- バブルソート
- マージソート
- クイックソート
- etc…
アルゴリズムの評価としての計算量
上記でアルゴリズムとはどんなものかを述べましたが、実際にプログラムを書くときには数種類のアルゴリズムからひとつを選んで実装するということになると思います。(ソーティングなどは、ライブラリの物を使うとは思いますが)
そのときに、アルゴリズムの評価軸として用いられるのが 計算量 です。アルゴリズムが任意の入力に対して正しい答えをだすという前提の上で、アルゴリズムを比較したいとなったときには、アルゴリズムの計算時間が少ない方が優れたアルゴリズムであると言えます。
もちろん、実際の計算時間は実行されるハードウェアの影響などを受けるので、抽象化して単純化した指標が計算量となります。
アルゴリズムの計算量は一般的に、入力データ数に比例することが多いです。そのためデータ数 $n$ を用い、計算量は $n$ の関数として表現することができます。
ここでは以下のように 表します。
$$ 計算量 = T(n) $$
具体例として、入力データ数と同じ回数だけの計算回数がかかるアルゴリズムがあるとします。
$n = 100$ の時に 計算回数が 100 回といった具合です。
その時の計算量は
$$ T(n) = n $$
とあらわすことができそうです。入力データ数の 2 乗に比例するのであれば、
$$ T(n) = n^2 $$
のように表すことができます。
他にも以下のように様々なケースが考えらるでしょう。
$$ T(n) = 5n^3 + 2n + 100 $$
$$ T(n) = 5\log{n} $$
$$ T(n) = 2^{n} $$
漸近計算量について
T(n) の計算量は具体的な数字ですが、一般的にアルゴリズムを評価する際には、もっとおおざっぱな漸近計算量が使われます。
$O(n)$ (オーダー n) や、 $O(n^3)$ (オーダー n の 3 乗) のような表記などを見たことがあるかもしれませんが、これらが 漸近計算量 となります。
ちなみに上記のようなオーダー記法を ランダウの記法 と言ったりします。
実際の計算量とこのおおざっぱな漸近計算量の対応の例を以下の表にまとめます。
| 計算量 $T(n)$ | 漸近計算量 $O(f(n))$ |
|---|---|
| $5n + 2$ | $O(n)$ |
| $5n^3 + 2n + 100$ | $O(n^3)$ |
| $5 \log{n}$ | $O(logn)$ |
漸近計算量を考える時は、T(n) の各項の中で発散が一番速いもの以外は無視して考えます。
発散の速さは以下のグラフを参照してください。横軸が n です。
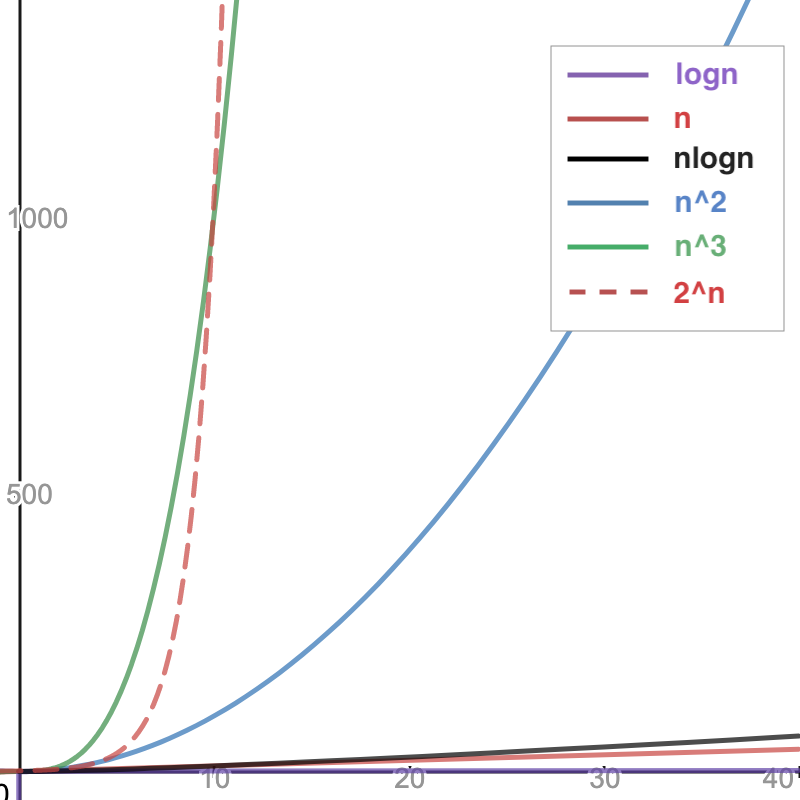
上のグラフから発散の速さは $logn < n < nlogn < n^2 < n^3 < 2^n$ のようになることがわかります。 そのため漸近計算量は $5n^3 + 2n + 100$ のような時は、n^3 の項以外は無視することになります。
無視できる理由としては、$n → \infty$ の極限を考えた時に、発散が遅い項の増加量の影響が無視できるほど小さいからからです。(全体の計算量に対して)
具体的に $T(n) → n^3 + 3n$ でデータ量 n が 10 → 100 に増えた時を考えると、以下の表のようになります。
| 変化 | 増加量 | |
|---|---|---|
| $T(n) = n^3 + 3n$ | $1010 → 1000100$ | $999270$ |
| $n^3$ | $1000 → 1000000$ | $999000$ |
| $3n$ | $30 → 300$ | $270$ |
上記からわかるとうり、 $3n$ の項が計算量 $T(n)$ に与える影響は非常に小さいため無視して考えることができます。
三種類の漸近記法 $O(f(n))$ $Ω(f(n))$ $Θ(f(n))$
前節で漸近計算量と、漸近記法 (ランダウの記法) について軽く触れましたが、漸近記法は 3 種類存在します。それぞれ少しずつ異なるため簡単に説明します。
$O(f(n))$
$O(f(n))$ は上記で触れたオーダー記法になります。アルゴリズムの計算量を評価する際に一番使われることが多いものです。
定義は以下のようになります。
正の定数 $N, C$ があり、すべての整数 $n \ge N$ において、$T(n) \le C \cdot f(n)$ のとき、$T(n) = O(f(n))$ とかける
上記の定義がどう言うことをいっているかを見ていきます
$T(n) \le C \cdot f(n)$ という式は、実際の計算量 $T(n)$ が 漸近計算量 $f(n)$ の定数倍より大きいことを表しています。
$T(n) = n^3 + 3n$ で $f(n) = n^3$ という具体的な例を考えると、
$$ n^3 + 3n \le C \cdot n^3 $$
となります。アルゴリズムの評価するという関係上、$n > 0$ のみ考慮すれば良さそうなので、式変形すると
$$ 1 + \frac{3}{n^2} \le C $$
となります。
上記の式から $n$ を 任意の$N$ 以上の任意の数値としても、以上の不等式を満たす $C$ はかならず存在します。
それは $n > 0$ という前提の元、左辺 $1 + \frac{3}{n^2}$は最大でも 4 にしかならないためです。($n=1$)
このような N, C が存在する時は、$n^3 + 3n = O(n^3)$ と書くことができるというのが、この定義が示していることです。
$O(n^4)$ としても、
$$ n^3 + 3n \le C \cdot n^4 $$
$$ \frac{1}{n} + \frac{3}{n^3} \le C \cdot n^4 $$
となり、$n = 1$ で最大でも $4$ にしかならないため、$n^3 + 3n = O(n^4)$ と書くこともできます。
これはつまり、$O(f(n))$ は多めに見積もった漸近計算量ということができます。多くても $f(n)$ の定数倍以内の計算量になるということです。計算量の上限を示しています。
具体例
$$ 4n^3 + 1 = O(n^3),\ \ 4n^3 + 1 = O(n^4) $$
$Ω(f(n))$
$Ω(f(n))$ の定義は以下のようになります。
正の定数 $N, C$ があり、すべての整数 $n \ge N$ において、$T(n) \ge C \dot f(n)$ のとき、$T(n) = Ω(f(n))$ とかける
$T(n) \ge C \cdot f(n)$ という式は、実際の計算量 $T(n)$ が 漸近計算量 $f(n)$ の定数倍より大きいことを表しています。
$O(f(n))$ と同様に $T(n) = n^3 + 3n$ で $f(n) = n^3$ という具体例で考えていきます。
$$ n^3 + 3n \ge C \cdot n^3 $$
$$ 1 + \frac{3}{n^2} \ge C $$
上記の色の左辺 $1 + \frac{3}{n^2}$ は $n$ の値がどんなに大きくても、1 以上になります。そのため $C$ が必ず存在するため、 $n^3 + 3n = Ω(n^3)$ と書くことができます。
$Ω(n^2)$ と言う場合も、
$$ n^3 + 3n \ge C \cdot n^2 $$
$$ n + \frac{3}{n} \ge C $$
となるため、左辺が n 以上になることから n 以下の 定数 C は必ず存在し、$n^3 + 3n = Ω(n^2)$ と書くことができます。
$Ω(fn)$ の場合は、少なめに見積もった漸近計算量ということができます。少なくても $f(n)$ の定数倍以上の計算量になるということです。計算量の下限を示しています。
念のため、$n^4$ の場合も見てみます。
$$ n^3 + 3n \ge C \cdot n^4 $$
$$ \frac{1}{n} + \frac{3}{n^3} \ge C $$
C は正の定数なので、1 以上なのですが、 $n → \infty$ のとき、左辺は 0 に収束するため、正の定数 C が存在しないケースがあるので、$n^3 + 3n \ne Ω(n^4)$ となります。
具体例
$$ 4n^3 + 1 = Ω(n^3),\ \ 4n^3 + 1 = Ω(n^2) $$
$Θ(f(n))$
上記の、$O(f(n)) ,\ Ω(f(n))$ は上限と下限を示していましが、$Θ(f(n))$ は制限が厳しく、一番正確な漸近計算量となります。
定義は以下の通りです。
正の定数 $N, C$ があり、すべての整数 $n \ge N$ において、$T(n) = C \dot f(n)$ のとき、$T(n) = Θ(f(n))$ とかける
これまでと同様に $T(n) = n^3 + 3n$ で $f(n) = n^3$ という具体例で考えていきます。
$$ n^3 + 3n = C \cdot n^3 $$
$$ 1 + \frac{3}{n^2} = C $$
となるので任意の正の定数 $C$ が存在します。$n → \infty$ でも $1$ に収束します。
そのほかのケースも見てみます。
$$ n^3 + 3n = C \cdot n^4 $$
$$ \frac{1}{n} + \frac{3}{n^3} = C $$
は、$n → \infty$ のときに、$0$ になってしまい正の定数 C が存在しないケースがあります。
$$ n^3 + 3n = C \cdot n^2 $$
$$ n + \frac{3}{n} = C $$
は、$n → \infty$ のときに、左辺が $\infty$ となってしまい収束しません。
具体例
$$ 4n^3 + 1 = Θ(n^3) $$
まとめ
今回は、アルゴリズムの評価方法でもある計算量についてまとめてみました。ざっくりとした知識しかなかったのですが、ちゃんと数学的に定義されているのを初めて知って理解が深まったような気がします。日頃なんとなく使っている知識の背景を知ることも重要だなと思いました。

