こんにちは、 @kz_morita です。

圏論について入門する記事の三回目です．

前回の記事はこちら．

• 圏論への入門 圏論とは
• 圏論への入門 圏の例としての順序集合

集合圏 Set とは

一つの集合を対象とし，集合間の写像を射とする圏のことです．

集合 A を 集合 B に移すような写像を $f: A \to B$ と書き，写像 $f$ は，$f(a) = b$ と表せるように，集合 A の要素 a を ただひとつの集合 B の要素 b に移すような関数を指します．

具体例でいうと，整数全体 $\mathbb{Z}$ を自然数全体 $\mathbb{N}$ に移すような写像 $f(x) = x^2$ などを考えることができます．

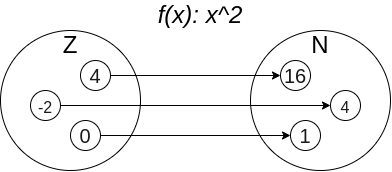
写像についておさらい

写像に大きく分けて以下の 3 つがある

• 単射
• 全射
• 全単射

単射

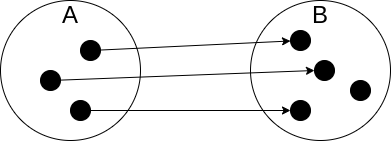
単射の定義は，以下の通りです．

$$ a \neq a' \ ならば \ f(a) \neq f(a') $$

集合 A の各要素がそれぞれ別の集合 B の要素に移されるような写像です．(同じところに移らない)

全射

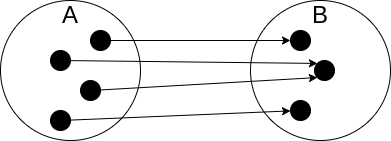
全射の定義配下のとおりです．

$$ 任意の \ b \ で \ b = f(a) \ が成立する $$

どういうことかというと，B のすべての要素に対しての写像が存在する写像です．

全単射

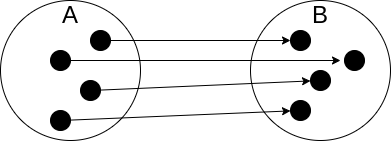
全単射は，全射の条件 + 単射 の条件で，異なる集合 A B 間のすべての要素が 1 対 1 対応しているような写像です．

すべての要素が 1 対 1 に対応しているため逆向きの写像も必ず存在します．

逆写像とよび，$f^{-1}$ のように表します．

圏としての集合

圏として考えるために，合成と恒等射について考えます．

合成

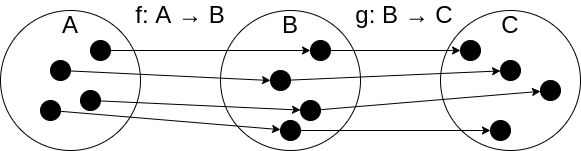
合成は，以下のように考えます．

$$ f \circ g = g(f(x)) $$

プログラムと同様に，内側から適用されていくイメージです．

恒等射

集合 A から 集合 A への恒等射 $1_A$ は，以下のように考えます．

$$ 1_A (a) = a $$

同じ要素に移す写像です． また，全単射の場合には，

$$ 1_A = f \circ f^{-1} $$

となります．

まとめ

今回は，集合を圏の 対象と考える集合圏 Set について記載しました．

次はモノイドあたりについて書いていこうと思います．