こんにちは、kz_moritaです。\
今回は、前回の続きです。
前回作成したプログラムをメモ化という方法で高速化してみます。
すでに計算したものをメモする
前回と同様ナップサックにアイテムを入れるかどうかの木構造を考えたときに、以下のようになったと仮定します。
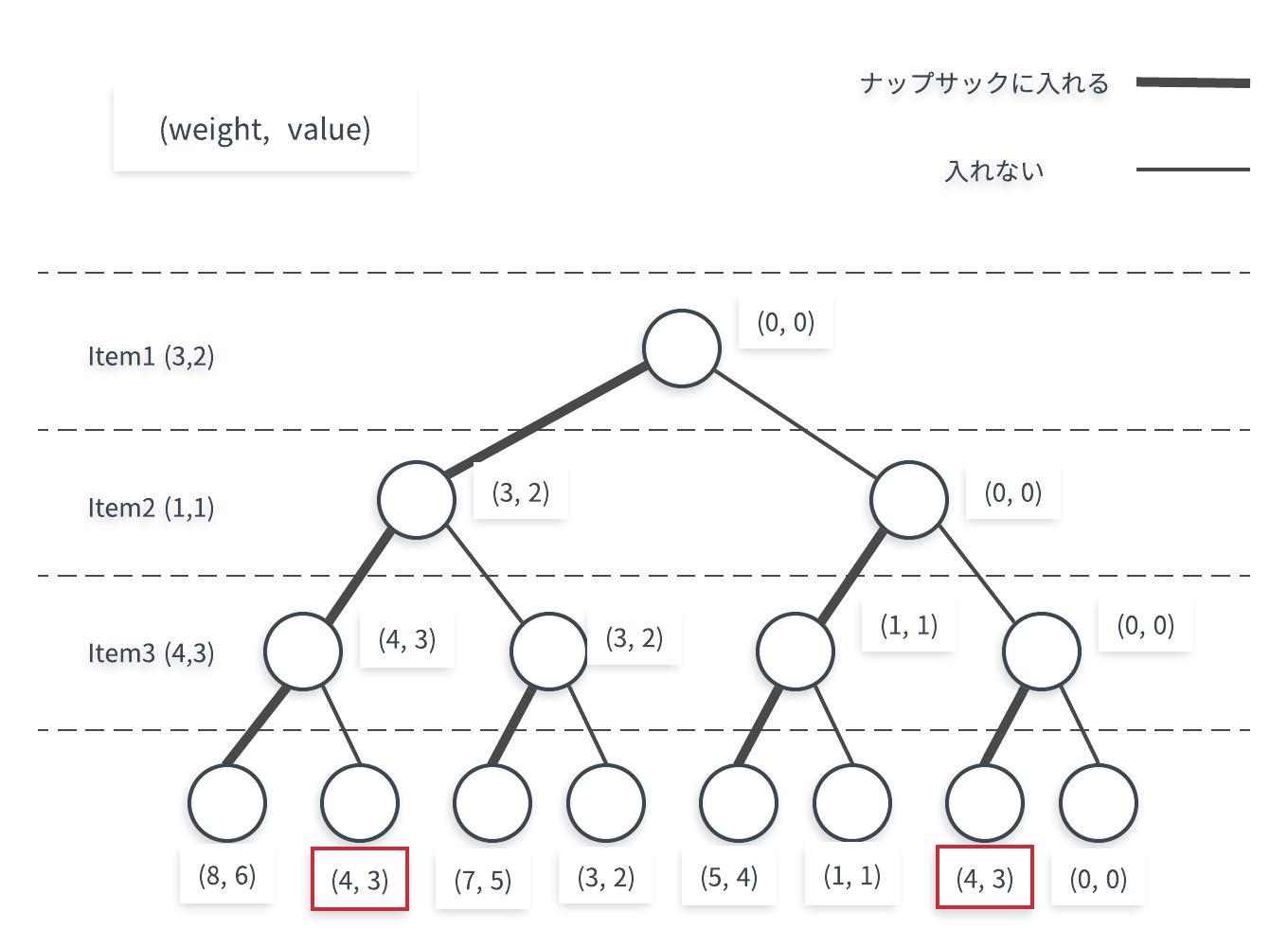
赤で囲った部分に注目していただくと、全く同じ (weight, value) になっていることがわかります。
これらのノードの下に続くノードたちは全く一緒のものになります。
つまり、ここは片方で計算し終えていれば再度計算する必要はありません。 よってこのノードの以下の計算結果をメモしておいて再利用することができます。
実装
それでは早速計算結果をメモする実装を行なっていきます。
今回大きく変わったのは、再帰的に計算した結果を memo に保持しておく必要があるため、 knapsack 関数を3引数でグローバルなtotalValueを更新するのではなく、int型の返戻値(アイテムの合計の価値) を返すように修正します。
そして再帰的に見ていく子ノードのアイテムを入れるorいれないについて、計算結果の大きい方をメモしていきます。
それでは以下にソースコードを記載します。
#include <iostream>
#include <vector>
#include <numeric>
using namespace std;
struct Item {
int weight { 0 };
int value { 0 };
};
vector<Item> items {
{ 3, 2 },
{ 4, 3 },
{ 1, 2 },
{ 2, 3 },
{ 3, 6 }
};
int capacity = 10;
// アイテムの数は精々100個、knapsackの容量の最大値を10000とした時に、
// 取りうる値は、0 ~ 各値に最大値なので
// +1 分の配列を用意する
int memo[101][100001];
int knapsack(int currentWeight, int index) {
// Check capacity
if (currentWeight > capacity) {
// Capacity Over なので、選択されないように負の大きい値を返す
return -99999;
}
// Check item size
if (items.size() <= index) {
return 0;
}
if (memo[index][currentWeight]) {
return memo[index][currentWeight];
}
Item item { items[index] };
const int ret { max({
knapsack(currentWeight + item.weight, index+1) + item.value,
knapsack(currentWeight, index+1)
}) };
memo[index][currentWeight] = ret;
return ret;
}
int main() {
int value = knapsack(0,0);
cout << value << endl;
return 0;
}
以下の部分で計算済みであれば、memoした値を返すように修正しています。
if (memo[index][currentWeight]) {
return memo[index][currentWeight];
}
まとめ
memo化という方法を使って、knapsack問題を効率化してみました。 次回はこのmemoテーブルに着目して、動的計画法という方法でknapsack問題を解いてみます。