こんにちは、 @kz_morita です。
圏論について入門する記事の4回目です。
これまでの記事はこちら
モノイドとは
モノイドとは、圏において対象がただ1つの圏のことを指します。
例としてあげると、実数 $\mathbb{R}$ (の集合) を対象とし加算を射とするような圏があげられます。
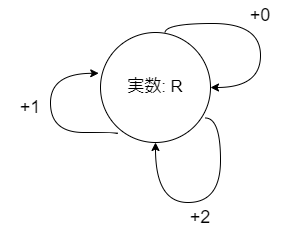
どんな加算をしても $\mathbb{R}$ の要素となるため対象は1つで、射が複数あります。
また、モノイドは対象が1つのため実質的に射の集合として捉えることができます。 前述の例だと、以下のような射の集合と考えられます。
$$ X = \lbrace +0, +1, +2, +3, … \rbrace $$
また、対象が1つであるためどの2つの射でも合成ができ、合成結果もモノイドの射の集合の要素となります。これを、モノイドの射の集合 $M$ をもちいて以下のように表します。
$$ \circ : M \times M \to M $$
$M \times M$ は集合の直積 ($M$ の要素すべての組み合わせ)を表し、それが $M$ への写像であるということです。
また、恒等射も考えることができます。
上記の射の集合の場合、$+0$ は恒等射ということができそうです。
モノイドの定義を圏論的に考えると以下のようになります。
モノイドは次の3つの組み合わせの事を言います。
$(M, \circ, 1_M)$
- M は 集合
- $\circ$ は、$\circ: X \times X \to X$ となる M上の演算
- $1_M \in M$ となる M の元
となり、下記の満たすものです。
$a,b,c \in M$ となる射において
- (結合律): $a \circ (b \circ c) = (a \circ b) \circ c$
- (単位律): $1_M \circ a = a = a \circ 1_M$
モノイドの圏
モノイドが対象とした圏も考えることができ、モノイド準同型 というものを射とする圏をモノイドの圏 Mon と呼びます。
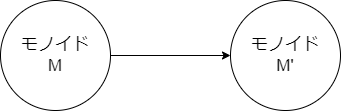
モノイド準同型とは以下のような定義です。
写像: $f: M \to M'$ が以下を満たす。
- Mの任意の要素 a, b について $f(a \circ_M b) = f(a) \circ_{M'} f(b)$
- $f(1_M) = 1_{M'}$
具体例を考えるために以下の2つのモノイドについて考えます。
- $(\mathbb{R}, +, 0)$
- 実数の集合を対象とし、+ (加算)を射とするモノイド。単位元は 0
- $(\mathbb{R}_{>0}, *, 1)$
- 正の実数を対象とし、* (乗算) を者とするモノイド。単位元は 1
これらのモノイド間の写像である、$f(x) = 2^x$ はモノイド準同型になります。
具体例で考えます。
まず$f(1_M) = 1_{M'}$ を考えると、
$f(1_M) = f(0) = 2^{0} = 1 = 1_{M'}$
となり条件を満たします。
つぎに、$f(a \circ_M b) = f(a) \circ_{M'} f(b)$ を考えると、
$a = 1, b = 2$ として考えると、 $f (1 + 2) = 2^3 = 2^1 * 2^2 = f(1) * f(2) $ となるため満たされます。
まとめ
今回は、モノイドとモノイドの圏である Mon について書きました。
圏のひとつであるモノイドですが、それ同士の関係性自体も圏として捉えられるという点でぐっと抽象度が高くなるため混乱しがちですが、具体例を考えると理解できるかと思います。
モノイドの圏について考えましたがモノイドそれ自体も圏であるため、より抽象化して 圏の圏 を考えられ、この後にでてくる 関手 について考えることができるためこのあたりは整理して理解しておきたいと思います。