こんにちは、 @kz_morita です。
圏論に入門する記事の6 回目です。
これまでの記事はこちら
Hom 集合
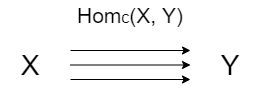
とある圏 C の2つの対象 $X, Y$ について、2つの対象の間の射は複数存在するが、その射の集合を Hom 集合 とよび、$Hom_C(X, Y)$ と表現します。
Hom 関手
とある圏Cに対してある特定の点A を固定してそこから各対象への Hom集合を取る操作はもとの圏C から 集合圏 Set への関手となり、Hom 関手 と呼ばれます。
最初 Hom 関手について聞いたときに、なんのことかよくわからなかったのですが図解して見るうちに理解できてきたので図をつかって説明します。
関手の定義のおさらい
関手の定義は以下の様なものでした。
圏C と 圏D において、以下の条件を満たす $F$ を関手 (functor) と呼ぶ。
- $C\ の射 \ f: X \to Y \ を \ D \ の射 \ F(f): F(X) \to F(Y)$ に対応させる
- $F (f \circ g) = F(f) \circ F(g)$
- $F(1_X) = 1_{F(x)}$
この定義にそって、特定の点A から各対象への Hom集合を取る操作が関手になるかを確認していきます。
射の対応関係
$C\ の射 \ f: X \to Y \ を \ D \ の射 \ F(f): F(X) \to F(Y)$ に対応させる
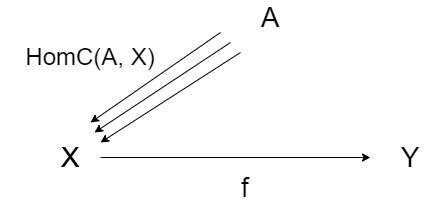
圏C の対象 X, Y と、射 $f: X \to Y$ を考えます。 任意の点 A を取り、その A から、対象 A への 射の集合を $Hom_C(A, X)$ とします。
同様に、AからYへの射の集合を $Hom_C(A, Y)$ とします。
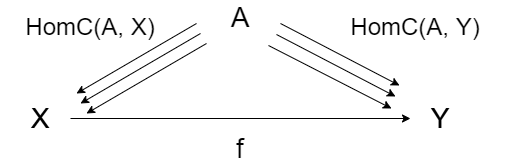
ここで、$Hom_C(A, X)$ の各射を $\lbrace a_1, a_2, a_3, …\rbrace$ と表すとすると、その射と f の合成はそれぞれ、$Hom_C(A, Y)$ の要素となります。
具体的には、以下のような b1 が存在するということです。
$$ b_1 = f \circ a_1 $$
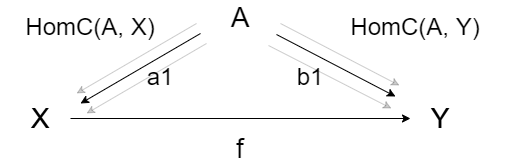
そのため、$f$ と $Hom_C(A, X)$ の各要素の射を合成する操作を $Hom_C(A, f)$ と表現すると
$$ Hom_C(A, f): Hom_C(A, X) \to Hom_C(A, Y) $$
となり、以下の関手の定義と対応します。
$C\ の射 \ f: X \to Y \ を \ D \ の射 \ F(f): F(X) \to F(Y)$ に対応させる
対応関係は以下のとおりです。
$$ F(f) = Hom_C(A, f) $$ $$ F(X) = Hom_C(A, X) $$ $$ F(Y) = Hom_C(A, Y) $$
射の合成の対応関係
$F (f \circ g) = F(f) \circ F(g)$
次は射の合成についての対応を見ます。 合成について確認するために、新たに圏C の対象の Z と、射 $g$ と $g$ の合成射の $f \circ g$ を考えます。
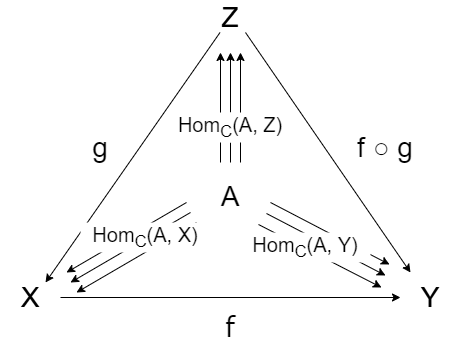
合成については、以下を満たせばよいです。
$F (f \circ g) = F(f) \circ F(g)$
まず左辺ですが、$Hom_C(A, f \circ g)$ は、$Hom_C(A, Z)$ の各要素と、射 $f \circ g$ を合成した射の集合のため、$Hom_C(A, Y)$ に当たります。
つまり、 $$ Hom_C(A, f \circ g): Hom_C(A, Z) \to Hom_C(A, Y) $$
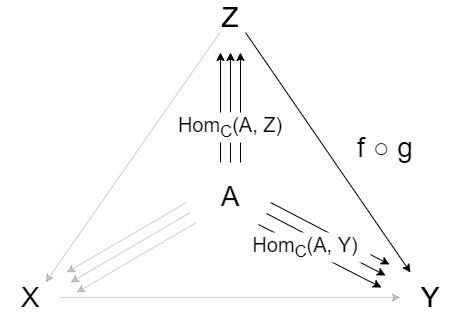
同様に、F(f) は
$$ Hom_C(A, f): Hom_C(A, X) \to Hom_C(A, Y) $$
F(g) は
$$ Hom_C(A, g): Hom_C(A, Z) \to Hom_C(A, X) $$
となるため、$Hom_C(A, f) \circ Hom_C(A, g)$ は 集合 $Hom_C(A, Z)$ を $Hom_C(A, Y)$ に移す集合圏の射となります。
これはすなわち、$Hom_C(A, f \circ g)$ と等しいため以下が成り立ちます。
$$ Hom_C(A, f \circ g) = Hom_C(A, f) \circ Hom_C(A, g) $$
恒等射の対応関係
$F(1_X) = 1_{F(x)}$
最後に恒等射について考えます。 こちらも合成を考えれば説明ができます。
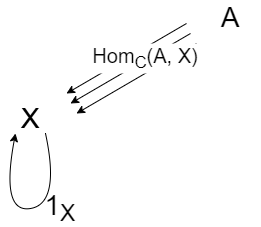
$Hom_C(A, 1_X)$ を 恒等射 $1_X$ と $Hom_C(A, X)$ の各要素の射を合成したものとし、$Hom_C(A,X)$ の各要素を $a_i$ と表現すると、
$$ a_i \circ 1_X = a_i $$
となるため、
$$ Hom_C(A, 1_X): Hom_C(A, X) \to Home_C(A, X) $$
となることがわかるため、$Hom_C(A, 1_X)$ 自体も恒等射になります。
$$ Hom_C(A, 1_X) = 1_{Hom_C(A, X)} $$
これで、関手の定義をすべて満たすことを確認できました。
まとめ
今回は、Hom関手 について図を交えながら理解したことをまとめました。
テキストで書かれていることがスッと理解できればよかったのですが、自分にとっては抽象的な話で理解が難しかったため図を書いて少しずつ理解しました。
パッと理解できないため進みがおそいですが少しずつ学び進めていこうと思います。