blog.foresta.me

圏論への入門自然変換

2023年4月17日 engineering

こんにちは、 @kz_morita です。

圏論に入門する記事の 7 回目です。

自然変換

自然変換は、関手の間同士の関係性で以下のような定義になっています。

$圏 \ C$ から $圏 \ D$ への関手 $F, G$ に対して $t$ が以下の条件をみたすときに、$F$ から $G$ への自然変換という

$t$ は $圏C$ の各対象 $X$ に対して、射 $F(X) \xrightarrow{t_X} G(X)$ を対応させる。
$圏C$ の任意の対象 X, Y 及び、任意の射 $X \xrightarrow{f} Y$ に対して、$G(f) \circ t_X = t_Y \circ F(f)$ が成り立つ
- $t_X$ は $t$ の $X成分$、$t_Y$ は $t$ の $Y成分$ と呼ぶ

自然変換は以下のように記述する

$$ F \overset{\text{t}}{\Longrightarrow} G $$

図で表すと以下のような関係性のことになります。

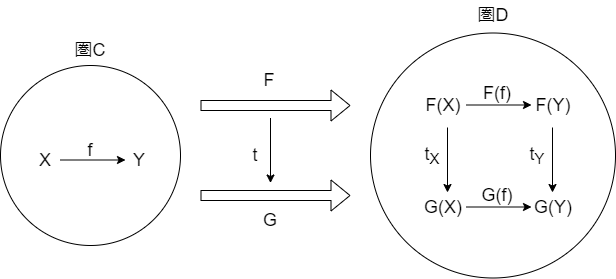
$圏 \ C$ から$圏 \ D$ への関手である $F, G$ の間の対応関係で、$X, Y$ それぞれに対して、$F(X) \to G(X)$, $F(Y) \to G(Y)$ を対応させるような変換 t のことを言います。

２つ目の定義の $G(f) \circ t_X = t_Y \circ F(f)$ も図で見るとわかりやすく、圏Dの左上 ($F(X)$) から右下 ($G(Y)$) へ射を合成した結果が一致することを示しています。

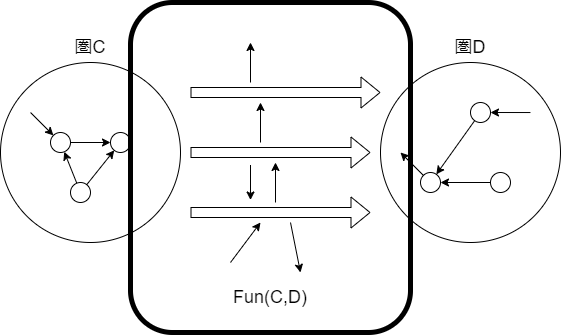
関手圏

上記で自然変換を書きましたが、関手が対象で自然変換が射であるような圏を関手圏と呼びます。

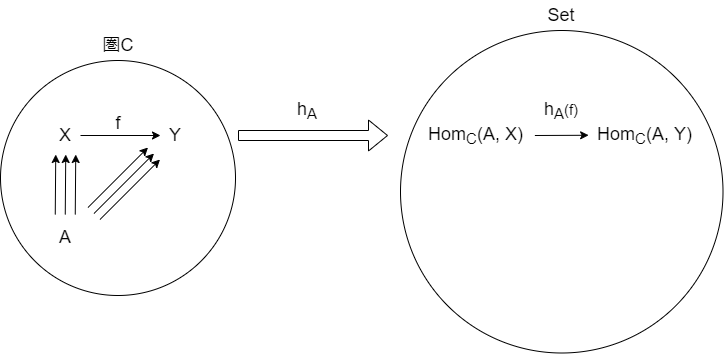
Hom 関手でみる自然変換

自然変換も抽象的なので具体的な例で見ていきます。Hom 関手間の自然変換について考えます。

まず Hom 関手とは以下のような任意の対象 A からX への射の集合 $Hom_C(A, X)$ を取る操作が、圏Cから Set への関手となるようなものでした。 $h_A(f)$ は、$Hom_C(A, X)$ の各要素と、f の合成を考えるものでした。

ここで任意の点 $A'$ をさらに追加で考えると以下のようになります。

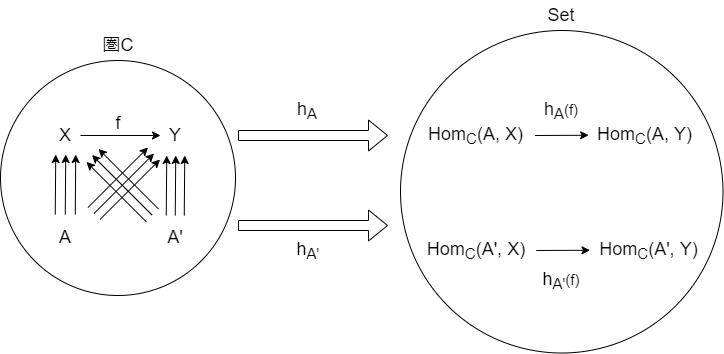
さらに、$A' \xrightarrow{a} A$ という射を考え、$h_a$ を Hom 集合と $射a$ との合成を取る操作と考えます。

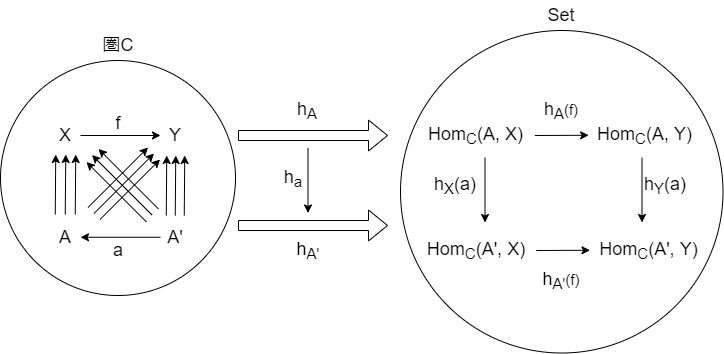
すると、以下の用になることが図からわかります。

$$ Hom_C(A, X) \xrightarrow{h_a} Hom_C(A', X) $$ $$ Hom_C(A, Y) \xrightarrow{h_a} Hom_C(A', Y) $$

この $h_a$ は以下に再掲する自然変換の定義を満たします。

$t$ は $圏C$ の各対象 $X$ に対して、射 $F(X) \xrightarrow{t_X} G(X)$ を対応させる。

$圏C$ の任意の対象 X, Y 及び、任意の射 $X \xrightarrow{f} Y$ に対して、$G(f) \circ t_X = t_Y \circ F(f)$ が成り立つ

1つ目はわかりやすいですが、2つ目も図からわかります。

$Hom_C(A, X) \xrightarrow{h_A(f)} Hom_C(A, Y) \xrightarrow{h_Y(a)} Hom_C(A', Y)$ と右回りに回るのと、$Hom_C(A, X) \xrightarrow{h_X(a)} Hom_C(A', X) \xrightarrow{h_{A'(f)}} Hom_C(A', Y)$ と左回りに回る2パターンを考えます。

$Hom_C(A, X)$ の 1要素の $射x$ について考えると前者は、 $$ h_Y(a) \circ h_A(f)(x) = (f \circ x) \circ a $$

後者は $$ h_{A'}(f) \circ h_X(a)(x) = f \circ (x \circ a) $$

となりますが、これらは結合律により等しくなるので2つ目の定義も満たします。

まとめ

今回は、自然変換についてまとめました。関手をさらに対象とみる関手圏をあつかったためより抽象度が上がった気がしますが、落ち着いて具体例でみると自然変換についても理解することができた気がします。

関連記事